编者按：本文节选自《深度学习理论与实战：提高篇 》一书，原文链接http://fancyerii.github.io/2019/03/14/dl-book/ 。作者李理，环信人工智能研发中心vp，有十多年自然语言处理和人工智能研发经验，主持研发过多款智能硬件的问答和对话系统，负责环信中文语义分析开放平台和环信智能机器人的设计与研发。

以下为正文。

本文介绍n步方法、TD-λ、Eligibility Trace和函数近似。

更多本系列文章请点击强化学习简介系列文章。更多内容请点击深度学习理论与实战：提高篇。

n步方法

MC方法是用Episode结束时的回报来作为更新目标，而TD(0)使用一步之后的回报来作为更新目标：

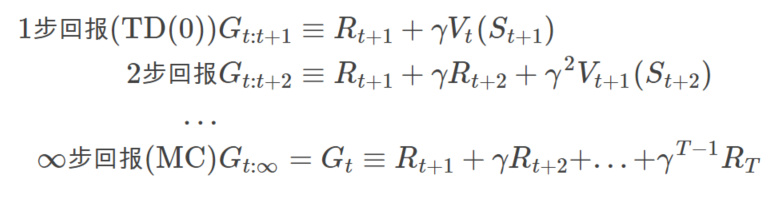
根据上面的推广，我们可以定义n步回报(n-step Return)为：

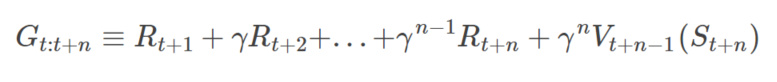
这些方法的backup diagram如下图所示。

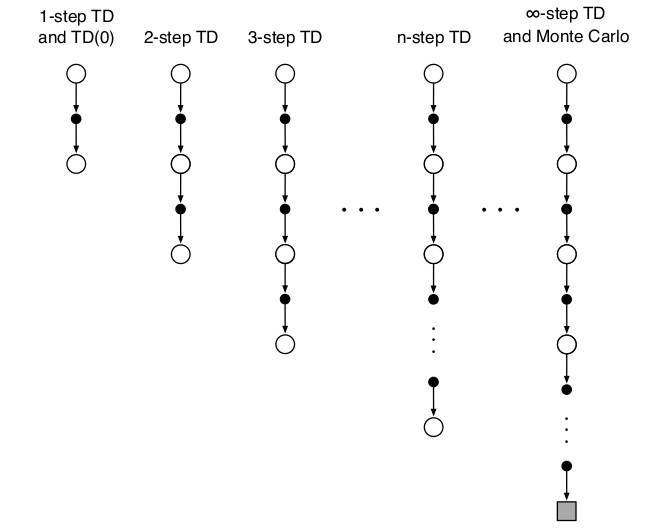
图：n步方法的backup diagram

有了n步回报之后，我们就可以n步TD学习算法的更新公式： Vt+n(St)←Vt+n−1(St)+α[Gt:t+n−Vt+n−1(St)],0≤t

下面是不同的n在一个19状态的Random Walk（由于篇幅，本书不介绍这个任务）中的对比效果如下图所示，可以看出n=1(TD)和n很大(MC)的效果都不如中间的某个n好。

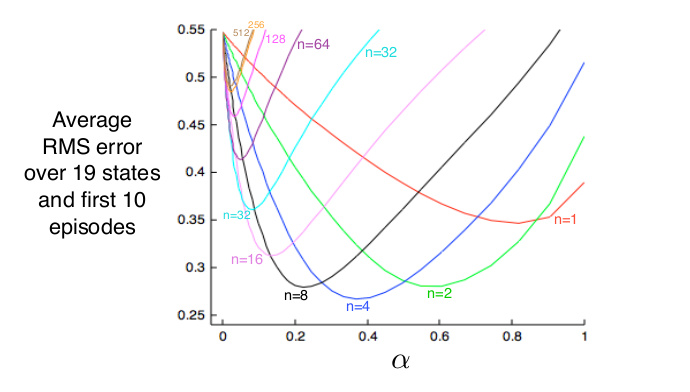
图：n步方法的比较

有了n步的预测，再加上ε-贪婪的策略提升，我们就可以实现n步的On-Policy策略n步SARSA算法。由于篇幅，我们就不讨论具体的算法了。同样的我们也可以使用重要性采样方法得到n步的Off-Policy算法。

TD-λλλ-回报

前面我们介绍了n步回报，不同的n有不同的效果，那么还有一种方法就是把多个n步回报进行加权平均。比如我们可以把2步回报和4步如图回报加权平均起来：

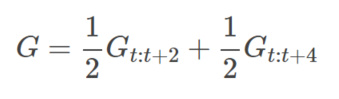
我们甚至可以把无穷多个n步回报加权平均起来，而λ-回报就是一种无穷多个n步回报的加权方式。无穷多个怎么加权呢？

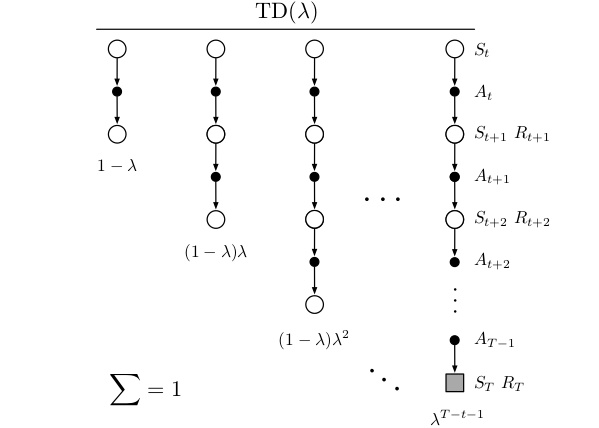
图：λ-回报

如上图所示，我们把无穷多个n步回报加权平均起来（因为当n大于T的时候，Gt:t+n就等于真实的回报Gt了。所有后面无穷项的系数都累加起来是λT−t−1，读者请先接受这个数字，我们后面会证明它。

从图中可以看出，1步回报的权重是1−λ，2步回报的是(1−λ)λ，3步回报是(1−λ)λ2，…，一共有无穷项：

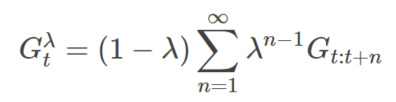
我们首先证明这无穷项的和是1。这需要一个简单的无穷级数公式：

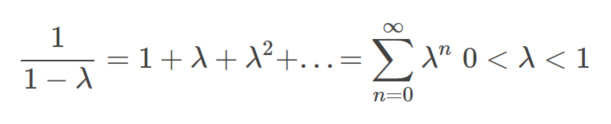
有了这个公式之后，我们就能计算所有回报的系数和：

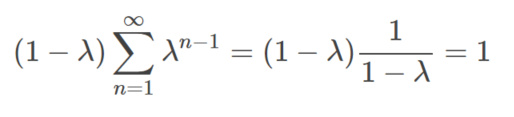
注意，因为当n=T-t及其以后Gt:t+n就等于真实的回报Gt了（因为到了Episode结束）。所以从n=T-t之后的项的回报是相同的，所以可以把后面无穷项合并起来：

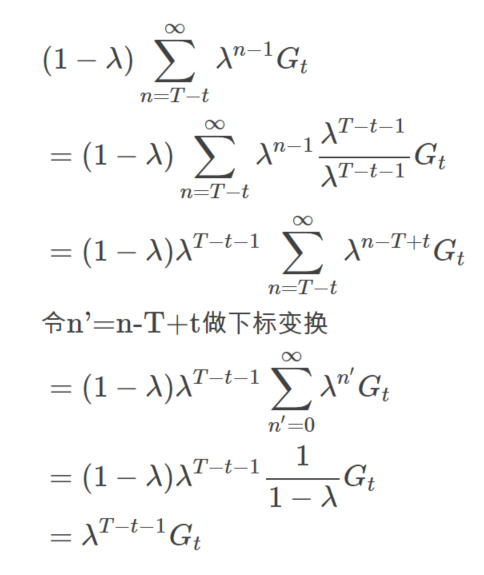
因此从n=1到T-t的n步回报的权重分配如图下图所示。这样，我们可以把Gtλ写出有限项的和：

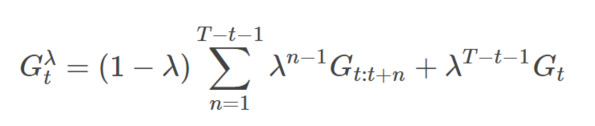
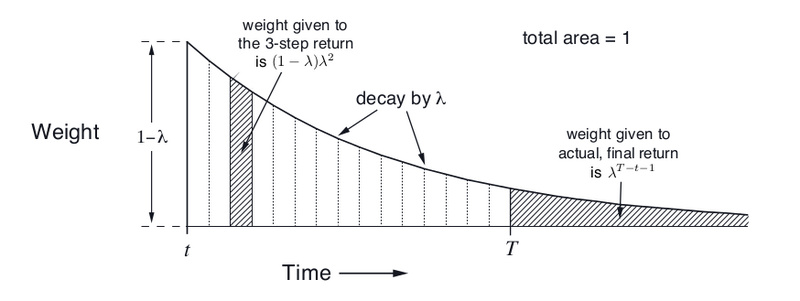
图：λ-回报的权重分配

有了λλ-回报的计算公式之后，我们就可以用它得到TD-λ算法的更新目标，从而就可以进行预测了。

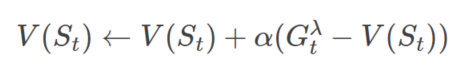
这就是著名的TD-λλ算法了，根据这个算法，Gerald Tesauro在1992年设计了TD-Gammon程序，它会学习西洋双陆棋(backgammon)，并且达到了人类顶尖高手的水平。

注意zhong这种TD-λλ算法是所谓的前向视角(Forward View)得出的，和MC一样，它要等到Episode结束才能计算，而且不能用于非Episode的任务。

另外，我们看一下λ的两个特殊值，λ=0λ=0和λ=1λ=1的特例。根据公式，当λ=0λ=0时，第二项是零，第一项只有当n=0时的系数是非零的1，因此变成了TD(0)算法。当λ=1λ=1时，只有第二项，因此变成了MC算法。

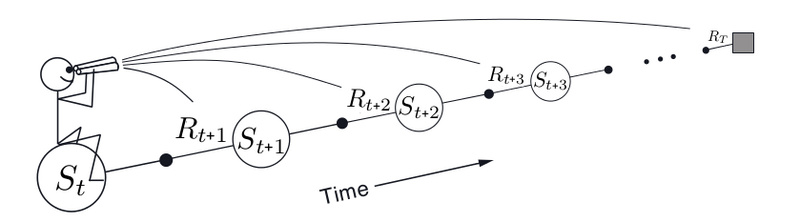
图：Forward View

Eligibility Trace